di Luca Cicali, pubblicato su Ocean4future http://www.ocean4future.org/archives/17058 (Per approfondire l’argomento si consiglia di leggere il libro di Luca Cicali “Oltre la curva”)

Teorie decompressive, storia e attualità: le grandi idee di Paul Bert e John Haldane

Ci sono due scienziati dell’800 ai quali dobbiamo le conoscenze attuali in materia di decompressione: Paul Bert e John Scott Haldane. I loro esperimenti, sfruttando cavie animali, portarono alla definizione di relazioni matematiche, poi impiegate negli algoritmi dei nostri odierni computer subacquei.

Il medico e professore universitario francese Paul Bert intuì per primo che la malattia da decompressione era dovuta all’eccesso di azoto disciolto nei tessuti e a un procedimento decompressivo troppo rapido. Usando dei cani come cavie, fece esperimenti di compressione e decompressione a varie velocità, evidenziando come la mortalità delle cavie variasse in funzione della velocità della fase decompressiva. Il professor Bert fu in grado di spiegare alcuni fenomeni basilari che sono legati alla patologia decompressiva. In particolare, comprese che la malattia da decompressione è dovuta alla formazione di bolle nei tessuti e nel sangue, determinata dall’eccessiva velocità della fase decompressiva. Inoltre che le bolle erano causate dall’azoto, che la respirazione di ossigeno puro aiuta in modo determinante sia la cura dei sintomi di malattia decompressiva, che lo smaltimento dell’azoto in eccesso e che una sosta a metà della profondità raggiunta è utile a scongiurare il pericolo di malattia da decompressione.

Ma in quel tempo la teoria della “congestione sistemica” era ancora salda nella comunità scientifica, e in un clima di forte controversia tra le due interpretazioni iniziò la costruzione del ponte di Brooklyn a New York. Nel 1867 fu fondata la società New York Bridge Company sotto la guida tecnica di John Roebling capo ingegnere.

Tre mesi più tardi l’ingegnere presentò il progetto di un ponte lungo circa 1.800 metri e con un impalcato sostenuto da quattro cavi sospesi tra due possenti torri di calcare e granito alte circa 84 metri, notevolmente più alte rispetto a qualsiasi altra struttura di New York della fine ’800. Le torri sarebbero state appoggiate sulla roccia, che si trovava a una profondità di 12 metri sotto la linea di galleggiamento sul lato di Brooklyn, e 22 metri sotto la linea di galleggiamento sul lato di New York. Nessun ponte era mai stato costruito a tale profondità, ed ecco l’importanza dei cassonisti.

Durante i tredici anni di lavori, dal 1870 al 1883, che furono necessari per il completamento del ponte di Brooklyn furono impiegati centinaia di operai e cassonisti, e più di venti di essi morirono per le conseguenze della malattia da decompressione.

Pochi anni dopo la morte di Paul Bert, nel 1900, tre scienziati Heller, Mager e Von Schrotter, fornirono la prima soluzione matematica per ottenere una stima dell’inerte che passa in soluzione nei tessuti, e successivamente viene rilasciato, in funzione della pressione ambiente e del tempo di permanenza in ambiente pressurizzato. Fu un lavoro imponente, grazie al quale essi giunsero a rappresentare matematicamente il fenomeno della saturazione e desaturazione dei tessuti da parte del gas inerte tramite la famosa equazione di tipo esponenziale.

Ma il contributo più determinante ai successivi sviluppi della teoria decompressiva fu dato dal fisiologo scozzese John Scott Haldane, nato nel 1860 ad Edimburgo, considerato il padre delle moderne teorie decompressive. Egli fu allo stesso tempo un uomo geniale e singolare; la sua più bizzarra caratteristica fu quella di essere egli stesso la cavia di molti dei suoi esperimenti, grazie ai quali poté verificare in prima persona l’attendibilità delle proprie intuizioni e l’efficacia delle proprie invenzioni.

Per meglio capire gli effetti delle respirazione di gas sull’organismo non trovava di meglio che … respirare egli stesso i gas oggetto dei suoi studi, con tutti i rischi che questa pratica comportava. Haldane iniziò quindi a interessarsi assiduamente alla malattia dei cassonisti, e a condurre test e verifiche in laboratorio e a bordo di una nave da guerra. Egli riprese il lavoro di Bert, lo analizzò accuratamente, e intraprese anch’egli esperimenti con cavie, utilizzando stavolta le capre al posto dei cani, intuendo che esisteva un valore massimo per la variazione di pressione alla quale l’organismo poteva esser sottoposto senza riportare danni una volta tornato alla pressione ambiente. Questa scoperta gli fu suggerita sia dagli esperimenti condotti sulle povere capre che dall’osservazione che gli operai cassonisti, che operavano in ambiente pressurizzato ed erano sottoposti ad una pressione ambiente inferiore a 2 bar (corrispondente a 10 metri di profondità), non riportavano danni risalendo in superficie, ovvero alla pressione di un atmosfera, anche se il turno di lavoro era stato molto lungo.

Altro significativo accorgimento di Haldane fu quello di schematizzare l’organismo secondo “compartimenti”, ovvero insiemi di tessuti che hanno simili caratteristiche rispetto alla velocità di assorbimento e rilascio dei gas. Questo consentiva di utilizzare l’equazione esponenziale e al tempo stesso tenere conto delle differenze tra tessuti, raggruppati in 5 diversi compartimenti caratterizzati da semi periodi paria a 5, 10, 20, 40 e 75 minuti.

Stabilì poi il suo principio più importante, quello che chiamò “rapporto di sovra-saturazione critica”, cioè il massimo valore ammissibile della variazione di pressione alla quale può essere sottoposto l’organismo umano per non riportare incidenti. Tale “Rapporto di Haldane” fu fissato al valore 2.

In base alle sue scoperte, intuizioni, approssimazioni e alla suddivisione dei tessuti in compartimenti, Haldane fu in grado di elaborare le prime tabelle decompressive, che furono pubblicate assieme ai fondamenti della sua teoria nel 1908. Le tabelle di Haldane furono quindi accettate universalmente e furono immediatamente applicate alle immersioni dalla Marina Militare Reale Britannica e nel 1912 anche dalla Marina Americana, che le utilizzò per più di mezzo secolo.

Le pietre angolari di Haldane

” … Misura ciò che è misurabile, e rendi misurabile ciò che non lo è … ”

 Galileo Galilei

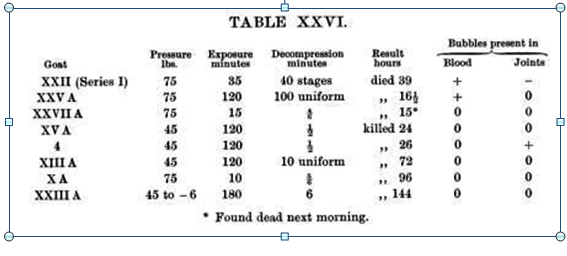
Haldane’s paper documents the effects of inadequate decompression strategies in lists of injured and killed goats. Source: The Journal of Hygiene, Vol. 8, No. 3 (Jun., 1908), pp. 342-443.

Nonostante sia passato tanto tempo dalla pubblicazione delle prime tabelle di Scott Haldane (1908), buona parte delle basi teoriche con le quali fu realizzato il modello sono ancora valide nei moderni modelli decompressivi.

Ricordiamo quindi brevemente i principi fondamentali fissati dal grande fisiologo scozzese:

a) l’organismo può essere schematizzato in gruppi di tessuti, o compartimenti, ognuno con il proprio semi-periodo. La saturazione di un compartimento è considerata praticamente raggiunta dopo 5 semi-periodi;

b) ad una variazioni istantanea della pressione della miscela respirata, la tensione di inerte nei compartimenti varia con legge esponenziale sia in fase di saturazione che di desaturazione;

c) è stabilito un rapporto massimo di sicurezza (detto “rapporto di Haldane”), tra la massima pressione ambiente raggiunta e la pressione alla quale si può risalire senza avere incidenti. Tale rapporto è pari a 2 per tutti i compartimenti. Se non si eccede il rapporto di Haldane non si ha formazione di bolle nel sangue e nei tessuti;

d) la fase di risalita di un’immersione va interrotta prima che la pressione ambiente si riduca più di quanto permetta il rapporto critico. La sosta deve durare per il tempo necessario a far diminuire la tensione del gas disciolto di quanto basta per permettere un ulteriore avvicinamento alla superficie senza violare il “rapporto di Haldane”, e così via sino alla superficie.

La strategia per evitare la malattia da decompressione è quindi legata alla proprietà dei tessuti umani di tollerare un livello di tensione di inerte superiore alla pressione ambiente, entro il limite del rapporto critico. 

Il subacqueo può quindi continuare a risalire in sicurezza finché non viola il rapporto critico neanche per un solo compartimento. Se riesce a raggiungere la superficie mantenendo questa condizione ha effettuato una immersione  entro la cosiddetta “curva di sicurezza”,  altrimenti dovrà osservare delle soste decompressive.

Robert Workman e i valori “M”

Il lavoro del dott. Workman fu sviluppato dal 1956 nell’ambito del team di ricercatori dell’Unità Sperimentale Subacquea della Marina statunitense (NEDU). Il rapporto di Haldane venne rimpiazzato da Workman con un parametro limite, detto valore “M” (Maximum), dove M è il valore della massima tensione di inerte accettabile in un dato compartimento affinché non si sviluppi la malattia da decompressione. M non è un valore costante ma dipende dal compartimento considerato e dalla profondità.

Quindi durante un’immersione, per essere in condizioni di sicurezza la tensione di inerte T in ciascun compartimento deve mantenersi sempre inferiore al valore M che corrisponde alla  profondità alla quale ci si trova.

M è pari alla somma di due addendi: il primo è un valore costante prefissato, M₀, e il secondo è ottenuto moltiplicando un coefficiente, (chiamato ΔM), per la profondità, (d=depth).

M= M_{0 +} ΔM x d

Ciò vuol dire che a profondità maggiori, anche il limite M accettabile per la tensione è maggiore. Ogni compartimento ha i propri coefficienti M₀ e ΔM.

Sono i valori M₀ a delimitare la curva di sicurezza, in quanto stabiliscono il massimo livello accettabile di inerte in un compartimento per giungere alla superficie, (d=0).

Il valore di ΔM fissa invece la velocità di variazione di M con la profondità.  Valori elevati di ΔM, come nel caso dei tessuti veloci, comportano un più veloce aumento di M con la profondità, quindi una maggiore “permissività” di accumulo di inerte con la profondità, ovvero tappe decompressive meno profonde.  Insomma, un compartimento risulta tanto più tollerante alla tensione di inerte accumulata, quanto più sono elevati i valori dei coefficienti M₀ e ΔM, e questo è ciò che accade per i tessuti più veloci.

Workman utilizzò 9 compartimenti, con tempi di emisaturazione che vanno da 5 a 240 minuti. Ciascuno dei compartimenti è quindi definito in base a tre parametri:

Se consideriamo un piano cartesiano che ha per asse orizzontale la tensione di inerte nei compartimenti, e per asse verticale la profondità, il valore M di ciascun compartimento può essere rappresentato da una retta, come mostrato in figura.

Ogni retta-valore M inizia in un certo punto dell’asse orizzontale corrispondente al valore M_0, e ha una certa inclinazione, come mostrato nella figura, (il numero dopo la lettera “C” rappresenta il compartimento, “T” il suo semiperiodo). Possiamo notare che i compartimenti con semi periodo (T) maggiore (cioè i tessuti più lenti) hanno maggiore inclinazione e un valore di M₀ più spostato a sinistra.

Che cosa vuol dire?  Semplicemente che tali compartimenti sono meno tolleranti alla tensione di inerte sia per il ritorno diretto in superficie (tempo di non decompressione inferiore) che a qualunque altra profondità (richiedono tappe di decompressione più profonde). Ciò è naturalmente compensato dal fatto che i tessuti più lenti richiedono molto più tempo per raggiungere elevati livelli di tensione di inerte disciolto. Proviamo ora a simulare un’immersione, ipotizzando per semplicità che esista solo un compartimento, nel nostro caso solo il n.3, che ha semi-periodo di 20 minuti e coefficiente M₀ pari a 2,19.

Facciamo l’ipotesi che il profilo di immersione sia stato tale che, all’istante di decidere la risalita, la tensione di inerte nel compartimento n.3 sia pari a 3,8 bar (è il computer subacqueo che stima questo dato).

Siamo dentro o fuori curva? Poiché 3,8 è maggiore del valore M₀ del compartimento 3 (pari a 2,19 bar), non è permesso il ritorno diretto alla superficie, quindi siamo fuori curva.

Qual è allora la profondità della prima tappa di decompressione necessaria?
Basta tracciare un segmento verticale che parte dal punto corrispondente a 3,8 bar sull’asse delle tensioni e va a incontrare la retta obliqua del compartimento n. 3.

A questo punto, come si vede nella figura, corrisponde sull’asse delle profondità il valore di 10,7 metri, e questa sarà la quota della prima tappa.  Durante questa tappa e durante quelle eventualmente successive, sarà necessario attendere finché la tensione scenda al di sotto di 2,19 per poter finalmente essere in superficie.

Ma in realtà l’organismo non è fatto di un solo tessuto o compartimento scelto a caso. Quindi, nel caso reale, per capire se l’immersione è con o senza decompressione è un pò più complicato. Si tratta cioè di comparare la tensione massima raggiunta da ciascun compartimento, nello stesso istante, con le rispettive tensioni di soglia M₀, verificare se sono state superate, e ripetere questi calcoli in continuazione durante l’immersione.

Se questa condizione si verifica anche per un solo compartimento l’immersione richiederà la decompressione. Complicato per un uomo ma semplice per un computer che fa migliaia di calcoli al secondo. Ma per fare questo ci vogliono degli algoritmi.

Possiamo adesso domandarci: cosa hanno a che fare i valori di M con il rapporto di sovra-saturazione critica di Haldane?

Moltissimo, i valori M di Workman sono i rapporti di sovra-saturazione di Haldane “modificati”, al punto che possiamo tracciare sul nostro piano una retta, che chiamiamo retta di Haldane, che rappresenta proprio il rapporto di Haldane espresso sotto forma di valore M, per il quale M₀ vale 1,58 e ΔM 0,258.

E’ come se Haldane avesse stabilito per tutti i compartimenti un valore M₀ pari a 1,58 bar, lo stesso valore M₀ che Workman assegna al compartimento “lento” n.6, con semi-periodo di 120 minuti. In pratica la vera novità di Workmann e del limite M fu una maggiore conservatività generale e l’adozione di criteri di massima sovra-saturazione di inerte specifici di ogni compartimento.

Il lavoro di Bühlmann

Il professor Bühlmann fece ulteriormente evolvere il lavoro di Workman, generando una versione ancor più conservativa dei valori M, in particolare per i tessuti intermedi, e rendendoli validi anche per immersioni in altura, e non solo al livello del mare.

L’originalità e l’importanza del lavoro di Bühlmann fu soprattutto nell’aver fissato dei criteri matematici per la determinazione dei coefficienti  M₀ e ΔM una volta stabilito il semi periodo. Ciò consente oggi di progettare agevolmente insiemi nuovi di compartimenti in numero e semi periodo caratteristico, ottenendo un modello decompressivo sempre coerente. Inoltre, esistono apposite formule di passaggio dai parametri di Bühlmann a quelli di Workman e viceversa, che consentono di esprimere agevolmente i nuovi valori M relativi ai compartimenti stabiliti da Bühlmann nella forma di Workman.

Il modello messo a punto dal professor Bühlmann riscosse un enorme successo applicativo, ed è stato utilizzato nei primi computer subacquei sviluppati e commercializzati fin dagli anni ottanta, e nella maggior parte di quelli oggi esistenti. A lui dobbiamo la sempre maggiore sicurezza delle nostre immersioni.

Qual è il segreto di tanta popolarità visto che, rispetto all’impostazione di Haldane, questo modello non presenta cambiamenti radicali?

Perché una diffusione così rapida e capillare dell’algoritmo di Bühlmann al polso di tanti subacquei nei mari di tutto il mondo?

La chiave del successo è contenuta in un libro, pubblicato per la prima volta in lingua tedesca nel  1983,  con il titolo “Decompression Sikness” che riporta la descrizione dettagliata delle basi teoriche del modello decompressivo di cui rappresenta un vero e proprio un vero e proprio manuale operativo. Il modello risultò determinante per il rapido  sviluppo di computer subacquei vista la relativa semplicità di implementazione dell’algoritmo decompressivo tramite un programma software per computer.

E’ sufficiente definire il numero di compartimenti e i loro semiperiodi, e le formule messe a punto da Bühlmann forniscono direttamente i parametri generatori dei valori di sovrasaturazione massima, (i parametri M₀ e ΔM). Un’occasione troppo ghiotta per non sfruttarla industrialmente e sviluppare velocemente il mercato dei computer subacquei.

Nella figura qui a lato iniziamo identificando la “zona di sottosaturazione”, costituita dal triangolo di colore celeste al di sotto della retta di saturazione tratteggiata. All’interno di questa zona la tensione di inerte nei tessuti è sempre inferiore alla saturazione, quindi i tessuti sono “sottosaturi” e la loro tensione è in fase crescente.  Questa è la zona nella quale inizia sempre un’immersione non ripetitiva, e nella quale ci si mantiene fino a quando la tensione di inerte è inferiore alla pressione ambiente di inerte, e quindi è in fase di crescita.

La parte di piano di colore bianco compresa tra la retta di saturazione e la retta (in rosso) del valore M del compartimento (nel nostro esempio il compartimento n.4 cioè C4), è la “zona di sovrasaturazione”, nella quale la tensione di inerte nei tessuti è maggiore della pressione ambiente di inerte, e quindi tende a decrescere. In questa zona i tessuti sono sempre in fase di desaturazione, mentre la tensione dell’inerte in essi disciolto resta al di sotto del limite M di sicurezza.

L’immersione sul piano tensione-profondità

E’ possibile e utile suddividere in varie zone il piano profondità-tensione utilizzato per tracciare le rette che rappresentano i valori M, al fine di caratterizzare adeguatamente le varie situazioni operative. A titolo di esempio, utilizziamo la retta di M del compartimento n.4 di Bühlmann, che ha un semiperiodo di 18,5 minuti. Riportiamo sul grafico anche la cosiddetta retta di saturazione, che rappresenta, per ogni profondità, il livello di tensione del compartimento una volta giunto alla saturazione.

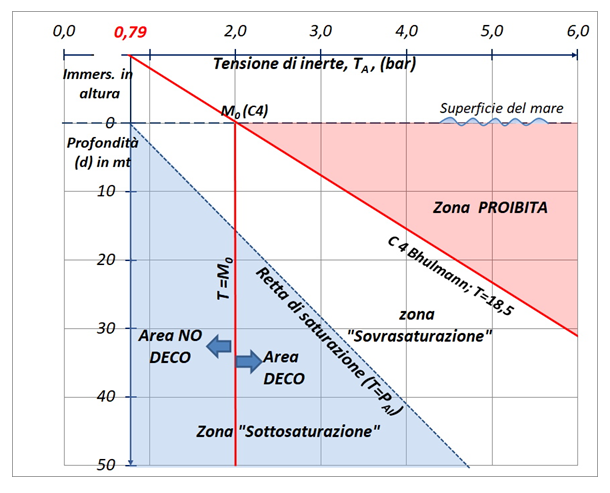Questa zona rappresenta lo spazio di desaturazione “utile”, un corridoio di sicurezza entro il quale debbono restare confinate sia le immersioni entro curva che quelle con decompressione, per non infrangere il criterio imposto dai valori M.

Infine abbiamo la “zona proibita”, nella quale ovviamente non ci si deve mai trovare, perché all’interno di essa la tensione di inerte nei tessuti, pur decrescendo, supera il massimo valore M ammesso per il compartimento considerato, e quindi è tale da causare teoricamente la patologia da decompressione.

Se tracciamo una retta verticale, (detta T=M₀)_, che parte dal valore M₀ del compartimento considerato otteniamo due diverse aree: la prima è l’area “NO-DECO”, a sinistra, e l’altra è l’area “DECO”, a destra. Queste due parti del piano rappresentano aree nelle quali ricadono immersioni entro curva, senza quindi obbligo di effettuare tappe decompressive, oppure fuori curva, con obbligo di effettuare soste  prima di raggiungere la superficie.   Se la retta verticale T=M₀ viene attraversata da sinistra a destra l’immersione diviene “con decompressione”, mentre l’attraversamento da destra a sinistra comporta il rientro entro curva. Fatte queste considerazioni, è possibile riportare sul piano tensione-profondità la corrispondenza tra tensione di azoto nei tessuti e profondità durante un’immersione, e identificare la situazione operativa in base alla zona o area in cui il punto corrispondente si trova.  Ciò consente di determinare, se si è in fase di saturazione, di desaturazione, se l’immersione è entro o fuori curva, e se stiamo effettuando una decompressione.

Luca Cicali